# 集中趋势度量

• 一组数据想其中心值靠拢的倾向和程度
• 测度集中趋势就是寻找数据水平代表值或中心值
• 不同类型的数据用不同的集中趋势测度值，低层次数据的测度值适用于高层次的测量数据，但高层次数据的测度值并不适用于低层次的测量数据。

# 众数

• 定义--
  • 一组中出现次数最多的变量值
  • 数学符号Mo
• 特点--
  • 不受极端值影响
  • 一组数据可能有0个,1个,多个众数。
• 应用--
  • 主要适用于分类数据
  • 主要用于数据量较多的时使用
• 计算--
  • Excel--MODE(num1,num2,...)

# 中位数

• 定义--
  • 排序后处于中间位置上的值
  • 数学符号 Me
• 特点--
  • 中位数是一个位置的代表值,不受极端值影响
  • 个变量值与中位数离差绝对值之和最小，即
• 应用--
  • 可以适用于一组数据分布偏斜程度较大时
  • 主要用于顺序型数据
• 计算--
  • 位置
  • 数值
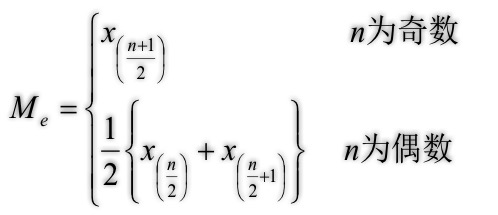
  • Excel-MEDIAN(num1,num2,...)

# 四分位数

• 定义--
  • 下四分卫数--排序后处于25%位置的数。
  • 上四分卫数--排序后处于75%位置的数。
• 特点--
  • 不受极端值影响
• 位置计算--
  • 简单公式:
  • 较为准确公式:
  • 依据中位数公式:
  • Excel:QUARTILE.INC(array,quart)
• 值判定--
  • 当位置数值是整数，对应数值就是位置上的数。
  • 当位置数值是x.5,对应数值就是两侧数值平均数
  • 当位置数值是x.25或x.75,对应数值Q=下侧值+(上侧值-下侧值)*比例

# 平均数(均值)

• 定义--
  • 集中趋势最常用的测度值
  • 一组数据的均衡点所在
• 特点--
  • 受极端值影响
  • 根据掌握的数据不同，平均数有不同的计算形式和公式。

# 平均数--简单平均数

• 定义--
  • 未分组数据计算的平均数称为简单平均数
• 计算方式--
  • 公式:
  • Excel:AVERAGE(number1,number2,...)

# 平均数--加权平均数

• 定义--
  • 根据分组数据计算的平均数为加权平均数
• 计算方式--
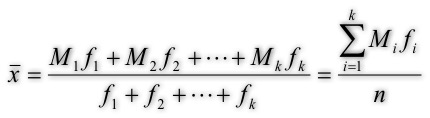
  • 公式:

# 平均数--几何平均数

• 定义--
  • 适用于特殊数据的一种平均数，主要用于计算平均比率。
  • 计算变量值本身是比率形式的。
• 应用场景--
  • 计算现象的平均增长率。
• 计算方式--
  • 公式:
  • Excel:GEOMEAN(number1,number2,...)

# 众数，中位数，平均数的关系

• 数据分布对称时：Mo=Me=x̄
• 数据分布左偏时：Mo>Me>x̄
• 数据分布右偏时：Mo<Me<x̄

# 离散程度

• 各变量值远离其中心的程度
• 离散程度越大，集中趋势测度值代表性越大，反之亦然。

# 异众比率

• 定义--
  • 非众数组的频率占总频数的比例。
  • 主要衡量众数对一组数据的代表程度。
• 特点--
  • Vr越大，众数代表性越差。反之则越好。
• 应用场景--
  • 主要用于分类数据。
• 计算方式--
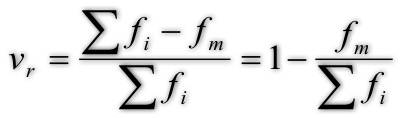
  • 公式:

# 四分卫差(内距，四分位距)

• 定义--
  • 用于衡量中位数的代表性
  • 反映了中间50%数据的离散程度
• 特点--
  • 不受极端值的影响
• 应用场景--
  • 顺序数据
• 计算方式--
  • 公式:

# 极差

• 特点--
  • 受极端值影响
  • 未考虑数据分布
• 适用场景--
  • 数值型数据
• 计算方式--
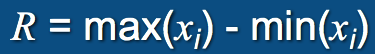
  • 公式:

# 平均差

• 定义--
  • 以平均数为中心，反映了每个数与平均数的平均差异程度，它能全面反映一组数据的离散情况。
• 特点--
  • 平均差越大，说明离散程度越大，反之亦然
  • 数学性质较差，应用少。
• 计算方式--
  • 未分组公式:
  • 组距分组公式:
• 引申-离差--
  • 每个数与平均数的距离。